ما هي المسائل الهندسية في اختبار القدرات؟

المحتويات
[عرض][إخفاء]- الهندسة المستوية (ثنائية الأبعاد)
- 1-مفهوم الأنماط الهندسية
- 2-المستقيمات
- 3-الزوايا
- 4-المثلثات
- 5- الاشكال الرباعية و المضلعات:
- 6-الدائرة:
- 7- المحيطات والمساحات و الحجوم:
- ما أهمية المسائل الهندسية؟
- ما أهمية المسائل التحليلية و الأحصائية؟
- كيف أتدرب على المسائل الهندسية؟
- ما هي طريقة حل المسائل الهندسية؟
- إذا كان الشكل خماسي منتظم، أوجد قياس الزاوية (س)
- ما قيمة (س) في الشكل الآتي
الهندسة هي أحد الفروع الأساسية للرياضيات التي تدرس القياس والمساحات وتشكيل الأشياء من وجهة نظر هيكلية. يتم دراسة الهندسة بشكل عام في جزأين: الهندسة المستوية (ثنائية الأبعاد) و الهندسة الفراغية (ثلاثية الأبعاد)
الهندسة المستوية (ثنائية الأبعاد)
الهندسة المستوية هي فرع من فروع الهندسة التي تدرس الأشكال وأبعادها على مستوى واحد. في الهندسة المستوية، يتم دراسة الأشكال المضلعة مثل المثلثات والمربعات والخماسيات وما إلى ذلك بالاضافة الى الأشكال الدائرية.
لهندسة الفراغية (ثلاثية الأبعاد)
تدرس الهندسة الفراغية الأشكال ثلاثية الأبعاد. في هذا الفرع من الهندسة، تتم دراسة الأشكال المخروطة و الكروية و المكعبة و المثلثة وما إلى ذلك.
القياس: مفهومه وأهميته في الهندسة
في قياس المستقيم، عادة ما يتم استخدام أدوات مثل المساطر العادية والمثلثة. باستخدام هذه الأدوات، يمكن للطالب بسهولة قياس طول خط أو حجم زاوية معينة.
ولكن في قياس الاشكال الغير مستقيمة، تُستخدم العلاقات الرياضية مثل قواعد الجيب وجيب التمام لحساب الأبعاد والأحجام.
1-مفهوم الأنماط الهندسية
الأنماط الهندسية هو سلسلة من الأشكال الهندسية المكررة حسب نمط معين، ويسمى الجزء الذي يتكرر بالنمط (وحدة النمط )،ويكون النمط إما بتغيير الشكل أو اللون،
وتشبه هذه الأنماط (المصنوعة من الأشكال الهندسية)، الأنماط المكونة من الأرقام لأن النمط يتم تحديده بواسطة قاعدة
2-المستقيمات
المستقيم : هو كائن رياضي يتشكل من نقاط متسامتة، له طول لانهائي وعرض يتناهى للصفر ويحتوي على عدد لا نهائي من النقاط،
، ويعطي المستقيم أقصر مسافة بين أي نقطتين. والمستقيم يمتد إلى ما لا نهاية من الجهتين.
3-الزوايا
الزاوية هي شكل هندسي ينتج من اتحاد شعاعين لهما نفس نقطة البداية، وتسمى هذه النقطة "رأس الزاوية"، ويسمى الشعاعان ضلعي الزاوية.
أنواع الزوايا
الزاوية الحادة
وهي التي يكون قياسها من صفر إلى أقل من 90 درجة.
الزاوية القائمة
وهي التي يكون قياسها 90 درجة
الزاوية المنفرجة
وهي التي يكون قياسها أكثر من 90 درجة إلى 180 درجة.
4-المثلثات
المثلث هو أحد الأشكال الأساسية في الهندسة، وهو شكل ثنائي الأبعاد مكون من ثلاثة رؤوس تصل بينها ثلاثة أضلاع،
أنواع المثلثات:
حسب أطوال الأضلاع
مثلث متساوي الأضلاع: هو مثلث جميع أضلاعه متساوية، وتكون جميع زوايا المثلث متساوي الأضلاع متساوية أيضا، وقيمة كل منها 60 درجة.
مثلث متساوي الضلعين: ويسمى أيضا متساوي الساقين، هو مثلث فيه ضلعان متساويان. الزاويتان المقابلتان لهذين الضلعين تكونان متساويتين أيضا.
مثلث مختلف الأضلاع هو مثلث أطوال أضلاعه مختلفة، زوايا هذا المثلث تكون مختلفة القيم أيضا.
حسب زواياه الداخلية
مثلث قائم الزاوية: له زاوية قياسها 90 درجة يدعى الضلع المقابل للزاوية القائمة بالوتر، وهو أطول أضلاع هذا المثلث.
مثلث منفرج الزاوية: له زاوية قياسها أكبر من 90 درجة وأصغر من 180 درجة
مثلث حاد الزوايا: كل زواياه قياسها أصغر من 90 درجة
حقائق عن المثلثات
مجموع زوايا المثلث
مجموع الزوايا الداخلية للمثلث يساوي 180 درجة.
الزاوية الخارجية للمثلث
الزاوية الخارجية للمثلث تساوي مجموع الزاويتين الداخلتين غير المجاورة لها.
5- الاشكال الرباعية و المضلعات:
المربع:
المربع هو شكل مغلق يتكون من أربعة جوانب متساوية الطول.
جميع زواياه 90 درجة.
الأقطار متساوية الطول ومنصفة عمودية لبعضها البعض.
يمكن أن يكون مستطيلًا أو معينًا.
مجموع زواياه الداخلية يساوي 360 درجة1.
المستطيل:
المستطيل لديه أربعة زوايا قائمة (90 درجة).
الأضلاع المتقابلة متوازية ومتساوية.
القطران يقسم المستطيل إلى مثلثين متساويين.
يمكن أن يكون مربعًا إذا كانت جميع زواياه 90 درجة1.
متوازي الأضلاع:
لديه أربعة أضلاع وأربع زوايا.
الأضلاع المتقابلة متوازية ومتساوية في الطول.
مجموع زواياه الداخلية يساوي 360 درجة.
القطران يقسم متوازي الأضلاع إلى مثلثين متطابقين1.
شبه المنحرف:
لديه أربعة أضلاع، حيث يتوازى اثنان منهما ويطلق عليهما “قاعدتي شبه المنحرف”.
الضلعان الآخران يسميان “جانبي شبه المنحرف”.
القاعدتان متوازيتان والأضلاع متساوية في الطول.
مجموع زواياه الداخلية يساوي 360 درجة.
المعين:
يشبه متوازي الأضلاع، لكن لديه أربعة جوانب متساوية.
القطران منصفان عموديان لبعضهما البعض.
جميع أضلاعه متساوية.
الأضلاع المتقابلة متوازية.
مجموع زواياه الداخلية يساوي 360 درجة.
6-الدائرة:
هي عبارة عن مجموعة من النِّقاط المرسومة على سطح مُعيَّن، وتبعُد جميعها المسافة نفسها عن نُقطة معيّنة تُسمّى المركز، في حين تُسمّى المسافة بين أيٍّ من هذه النّقاط ومركز الدّائرة بنصف قُطر الدّائرة
اما القطر هو هو يمثّل ضعف هذه المسافة،
7- المحيطات والمساحات و الحجوم:
المحيط
يتم حساب محيط الشكل الهندسي بجمع طول جميع جوانب الشكل.
المساحة
المساحة تعني الفراغ الذي يحتله شكل ما، ويتم حساب المساحة بضرب طول الشكل في عرضه.
الحجم
يتم حساب حجم الشكل الهندسي ثلاثي الأبعاد بضرب طول وعرض وارتفاع الشكل.
ما أهمية المسائل الهندسية؟
تكمن أهمية المسائل الهندسية في معرفة قدرة الطالب على التعرف على الاشكال الهندسية و قياس المحيط و المساحة و اطوال الاضلاع و قياس الزوايا
كما تعكس المسائل الهندسية مدى قدرة الطالب على التعرف على الاشكال الهندسية والقياس ،اهمية القياس في الهندسة عالية جدا حيث تعتبر القياسات الدقيقة مهمة جدا
ما أهمية المسائل التحليلية و الأحصائية؟
تكمن أهمية المسائل الحسابية في معرفة قدرة الطالب على التعامل مع العمليات التحليلية و الأحصائية وتمكن الطالب من تحليل البيانات و دراستها و استنتاج بعض النتائج و الحقائق منها
كما انها وسيلة مضمونة لتحليل الكم الكبير من البيانات والوصول الى نتائج دقيقة
كيف أتدرب على المسائل الهندسية؟
إذا أردت أن تتدرب على المسائل الهندسية هناك خطوات مهمة عليك القيام بها لتتمكن من إتقان فنيات ومهارات المسائل الهنسية وتتمكن من تحقيق درجة ممتازة في القسم الكمي في اختبار القدرات:
التسجيل في منصة اختبارات التي تتيح لك التدرب على هذه المهارة وكل مهارات اختبار القدرات باستخدام الذكاء الاصطناعي وتساعدك على تحسين مستواك في المسائل الهندسية.
التعود على قراءة السؤال بشكل سليم وبدقة.
كثرة التدريب المستمر.
التعرف على الأشكال الهندسية وخصائصها
دراسة الأشكال الهندسية ثنائية الأبعاد مثل المربعات، المستطيلات، المثلثات، والدوائر.
دراسة الأشكال الهندسية ثلاثية الأبعاد مثل المخروط و المكعبو الأسطوانة
تعلم خصائص هذه الأشكال، مثل الزوايا والمحيط والمساحة.
التدرب على حل المسائل الهندسية
ما هي طريقة حل المسائل الهندسية؟
لحل المسائل الهندسية بشكل صحيح، يجب على الطالب أن يحسن قراءة السؤال، ويفكر بشكل سريع ودقيق في كيفيّة حله، سنريكم الآن بعض أسئلة المسائل الهندسية وطرق حلّها..
إذا كان الشكل خماسي منتظم، أوجد قياس الزاوية (س)
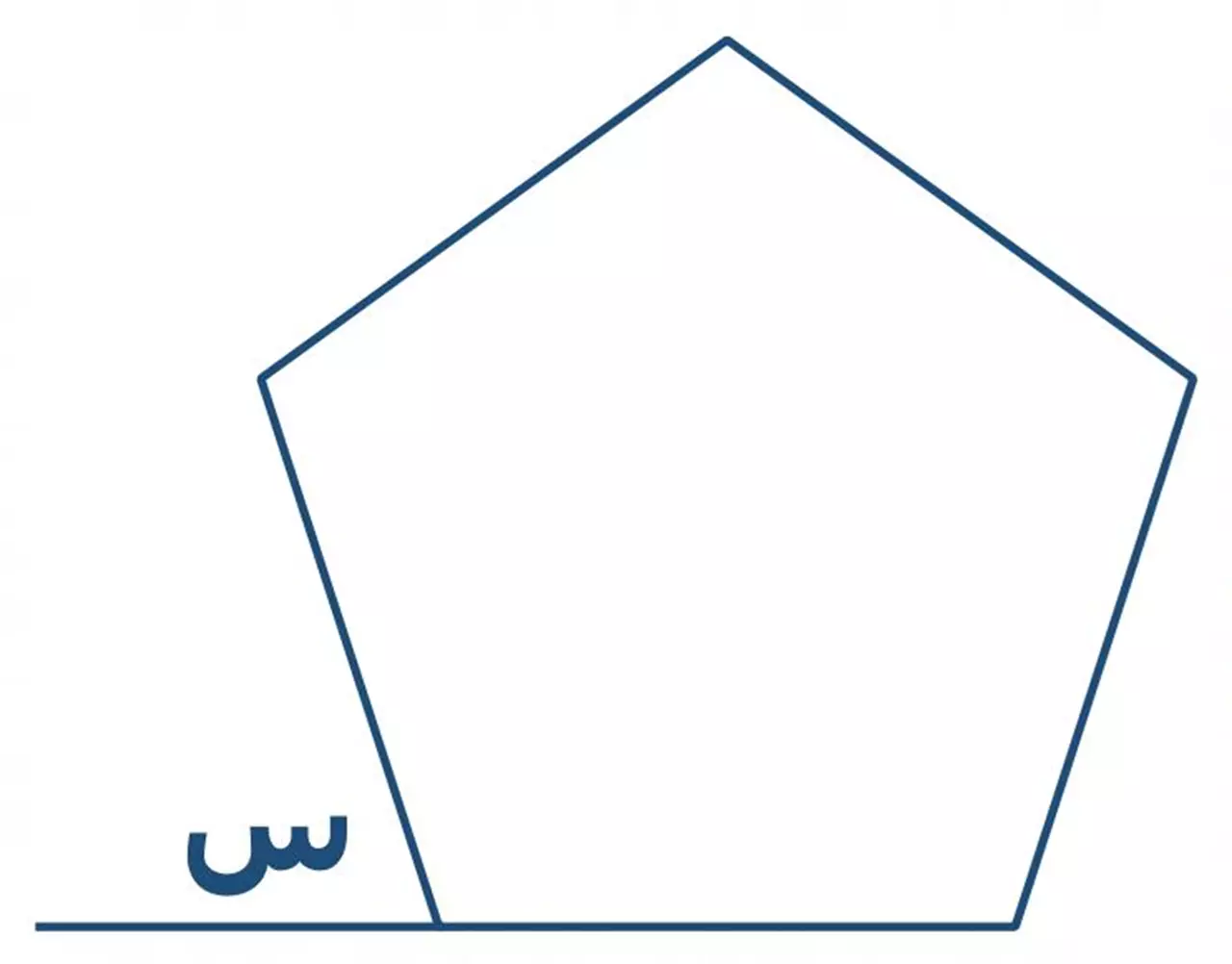
أ) 72
ب) 70
ج) 60
د) 108
الحل:
٧٢
طريقـة الحل
"مجموع قياس الزوايا الداخلية للخماسي المنتظم = ٥٤٠"
قياس الزاوية الواحدة = ٥٤٠ ÷ ٥ = ١٠٨
= ١٨٠ - ١٠٨ = ٧٢
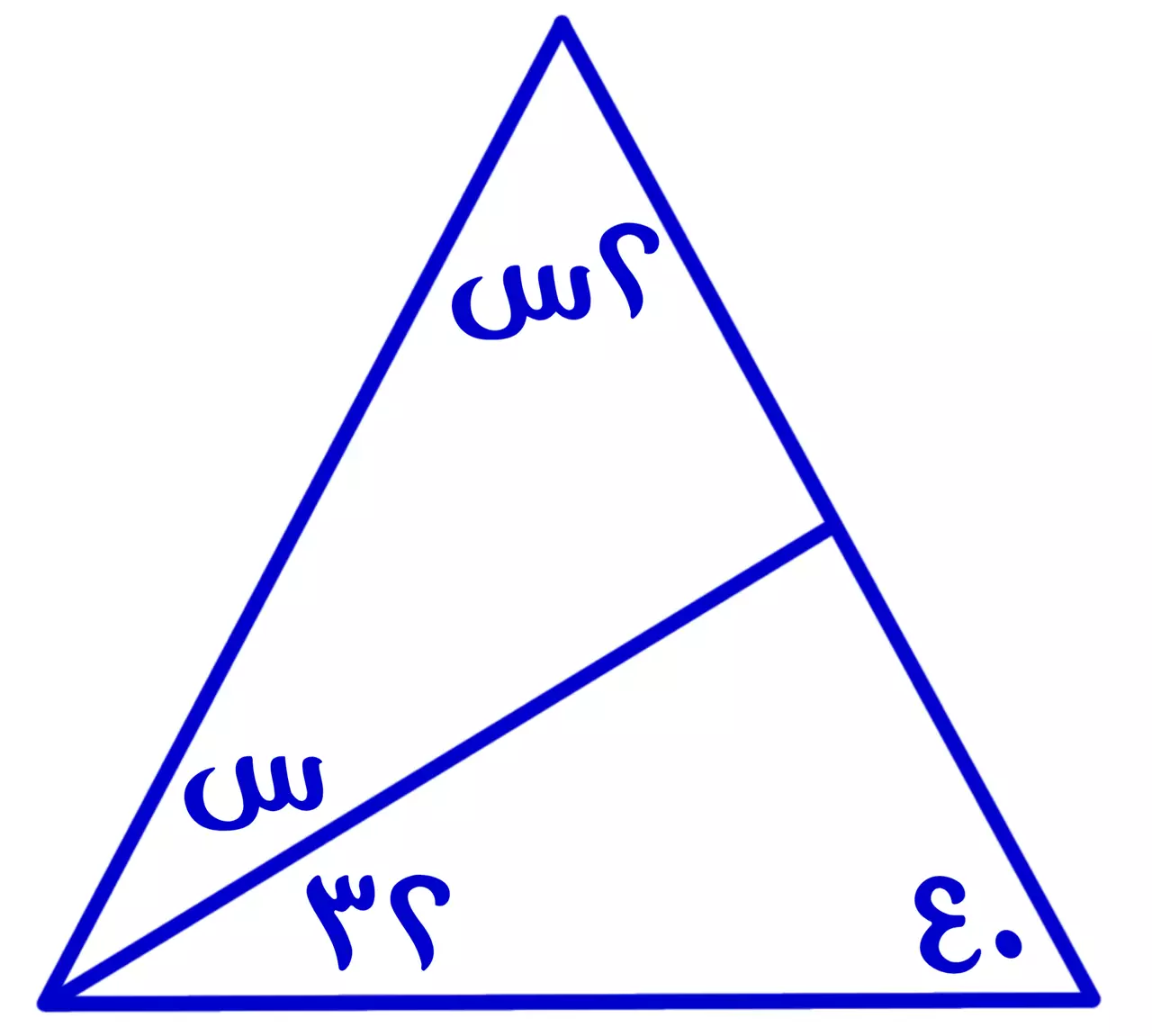
ما قيمة (س) في الشكل الآتي
أ) 36
ب) 32
ج) 40
د) 80
الحل:
٣٦
طريقـة الحل
س + ٢س + ٤٠ + ٣٢ = ١٨٠
٣س = ١٠٨
وإلى هنا نكون قد تحدثنا في هذه المقالة عن المسائل الهندسية في اختبار القدرات العامة وناقشنا أبرز المواضيع المتعلقة بها. تحدثنا في هذه المقالة عن أهمية المسائل الهندسية وأهم المهارات المطلوبة لحلها في اختبار القدرات. نتمنى لكم التوفيق في استعدادكم لاختبار القدرات.